题目内容
（请给出正确答案）
设曲面M上的一条曲率线C：x(s)(s为弧长)，它的每一点处的从法向量V3(s)与曲面在该点处的法向量n(s)成定角，且V3(s).n(s)≠±1(即V3s(s)不平行于n(s))．证明：C为平面曲线．
如果结果不匹配，请 联系老师 获取答案
更多“设曲面M上的一条曲率线C：x（s)（s为弧长)，它的每一点处…”相关的问题
设k(s0)≠0．证明：曲线C：x(s)(s为其弧长)与已给球面(球心为m)在s0有2阶接触
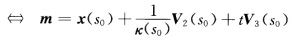其中t可以任意选定．上式右边当固定s0时得到一条直线，称为曲线x(s)在s0处的曲率轴或极轴，而点
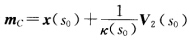称为曲率中心，以曲率中心为圆心、
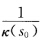为半径的圆落在密切平面上，称为曲线x(s)在s0处的密切圆(见习题1．4．3图)．(2)设k(s0)≠0，τ(s0)
设曲面M：x(u，v)上无抛物点，并设M的一个平行曲面为M：x(u，v)=x(u，v)+λn(u，v)，n(u，v)为x(u，v)处的单位法向l量，其中λ为充分小的常数，使1一λH+λ2KG≠0．证明：可选M的法向量n，使M的Gauss(总)曲率KG与平均曲率H分别为
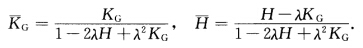
设曲线C：x(s)(s为弧长)为常挠曲率曲线．证明曲线
：
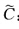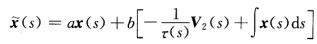为x(s)的Bertrand侣线，其中a，b为常数，k，τ，V2分别为x(s)的曲率、挠率和主法向量，x(s)为其本身的从法向量，即x(s)=V3(s)．
设常Gauss曲率曲面M：x(u，v)的第1基本形式为
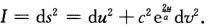．曲面
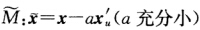证明：
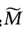与M有相同的Gauss曲率，但对应点的切平面互相正交．
设M为R3中的C4正则曲面，x(u1，u2)为其参数表示，P0∈M，且满足：(1)KG(P)＞0，即P0点的Gauss(总)曲率为正的；(2)在P0点，函数k1达到极大值，同时函数k2达到极小值，则P0为M的脐点．这和以下条件等价：设M为R3中的C4正则曲面，x(u1，u2)为其参数表示，P0∈M，且满足：(1’)P0为非脐点；(2’)在P0点，函数k1达极大值，同时函数k2达极小值．则KG(P0)≤0．
证明：曲面
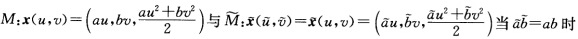在点(u，v)处Gauss(总)曲率相等．但M与
在此对应下未必为等距映射．问(a，b)与
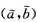满足什么关系时，M与
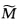在此对应下等距？
设曲面M：x(u，v)=(ucosv，usinv，lnu)与
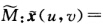(ucosv,usinv，v)在对应(u，v)→(u，v)下，Gauss(总)曲率相等，但此对应不是等距映射．
设R3中C2曲面M在等温参数{u，v}下，第1基本形式：I=ds2=E(du2+dv2)=λ2(du2+dv2)，E=G=λ2 (λ＞0)． (1)Laplace算子表达式为
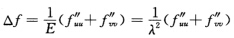其中f为M上的C2函数； (2)Gauss曲率为
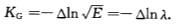
证明：具有常曲率k≠0的挠曲线x(s)为Bertrand曲线(s为弧长)，且x(s)的侣线
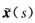是x(s)的曲率中心的轨迹；并且
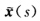的曲率
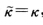，挠率
